Online-Team-Wettbewerb 2016 Aufgaben für die Sekundarstufe II (EF, Q1, Q2)

1. Aufgabe (Alles ist Mathematik - Zerlegungen überall):

a)
Zerlege die Zahl 18 in drei Summanden.
Wenn man diese Summanden der Größe nach ordnet, unterscheiden sich benachbarte Zahlen immer um den gleichen Wert.
Finde möglichst viele Zerlegungen.
Beispiel: 9 = 1+3+5.

b)
Zerlege die Zahl 125 so in fünf Summanden, dass folgende zwei Bedingungen erfüllt sind:
(1) Alle Summanden sind natürliche Zahlen und größer als Null.
(2) Ordnet man sie der Größe nach, unterscheiden sich benachbarte Zahlen immer um den gleichen Wert.
Bestimme alle möglichen Zerlegungen und begründe, warum es außer denen von dir genannten keine weiteren Zerlegungen gibt.

c)
Zerlege die Zahl 2016 so in sechs Summanden, dass die folgenden drei Bedingungen erfüllt sind:
(1) Alle Summanden sind natürliche Zahlen und größer als null.
(2) Ordnet man sie der Größe nach, so unterscheiden sie sich immer um zwei.
(3) Die einzelnen Summanden sind alle ungerade.

d)
Nun soll die Zahl 2016 so in sechs Summanden zerlegt werden, dass die folgenden Bedingungen erfüllt sind:
(1) Alle Summanden sind natürliche Zahlen und größer als null.
(2) Ordnet man sie der Größe nach, so unterscheiden sie sich immer um die gleiche Zahl.
(3) Die einzelnen Summanden sind alle ungerade.
Bestimme alle möglichen Zerlegungen und begründe, warum es außer denen von dir genannten keine weiteren Zerlegungen gibt.

e)
Eine beliebige dreistellige natürliche Zahl mit unterschiedlichen Ziffern habe die Form abc. Vertauscht man die Ziffern so erhält man cba. Zieht man nun die größere von der kleineren ab erhält, mal als Differenz xyz. Addiert man zu dieser Differenz die Spiegelzahl zyx so erhält man unabhängig von den gewählten Ziffern das Ergebnis 1089.
Beweisen Sie diese Eigenschaft für beliebige Zahlen dreistellige Zahlen abc mit a > c und c ≠ 0.

2. Aufgabe (Erbfall):

Der eigensinnige Onkel Donald will seinen Neffen und Nichten Oliver, Sue-Allen, Wayne und Nancy ein in der Wüste gelegenes, 100 Hektar großes, nutzloses quadratisches Grundstück vorzeitig übereignen.

Er ist schon etwas vergesslich, aber er ist sicher, dass sich Oliver als Ältester in guter beruflicher Position befindet und deshalb den kleinsten Anteil bekommen soll. Als Freund geometrischer und arithmetischer Spielchen will er, dass  keine zwei Erben einen gleich großen Anteil in dreieckiger Form bekommen sollen. Außerdem bestimmt er, dass Olivers Anteil die ganze östliche, Sue-Allen die vollständige südliche, Wayne die westliche und Nancy die ganze nördliche Begrenzungsseite des quadratischen Grundstücks umfassen soll. Wenn o, s, w und n die Flächenanteile der Nichten und Neffen mit entsprechenden Initialen ihres Namens sind, dann könnten die Verhältnisse der Anteile o:w = 1:4 und s:n = 3:2 sein. Es könnte ihm auch gefallen, wenn der Aufteilungsschlüssel o:n = 1:4 und s:w = 2:3 wäre. Falls es eine Lösung mit Verhältnissen aus den Zahlen 1, 2, 3 und 4 gibt, möchte er, dass der Unterschied zwischen dem größten und dem Anteil für Oliver möglichst klein ist.

a)
Überprüfen Sie seine Überlegungen und lösen Sie dieses Problem.  

b)
Welche Dreiecksgrundstücke nach Donalds erster Überlegung sind ggfs. spitz- bzw. stumpfwinklig?
Argumentieren Sie mit möglichst geringem Rechenaufwand.

3. Aufgabe (Probleme des Teilens):

Sabine und Bastian streiten sich über die Entscheidbarkeit der Teilbarkeit von Summen zweier Potenzen mit gleichem Exponenten. Während Sabine zu leichter (sprich: schneller) Entscheidbarkeit tendiert, ist sich Bastian nicht so sicher und wählt als Beispiel:

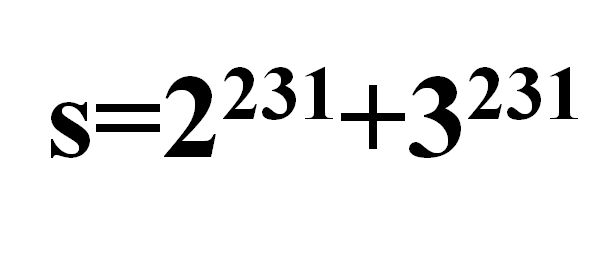
und die Frage, wie es denn beispielsweise mit der Teilbarkeit durch die ersten fünf Primzahlen stehe.

Sabine spontan: "Na klar, s ist ungerade als Summe einer geraden und einer ungeraden Zahl; also teilt 2 nicht s."

Bastian: "Ok, aber wie steht es mit den anderen?"

Äußern Sie sich dazu.

4. Aufgabe (Eine Schifffahrt ist lustiger):

Die Mathe-Treff Redaktion macht einen Betriebsausflug zur Mosel.
Dort soll eine Schifffahrt von Bernkastel-Kues nach Zeltingen-Rächtig stattfinden.

Zunächst kommt das Schiff der Reederei an, mit dem unsere Gruppe losfährt.
Während diese ablegen, kommt das Schiff einer konkurrierenden Reederei an und legt ca. eine Minute später in Bernkastel-Kues ab. Das Schiff unserer Redaktionsmitglieder ist sogar etwas schneller als das Schiff der dahinter fahrenden Konkurrenz.

Dennoch holt das hinterherfahrende Schiff unser Schiff noch vor dem Ziel ein.

© 2016 Mathe-Treff der Bezirksregierung Düsseldorf.
Ein Nachdruck oder eine Veröffentlichung auf gedruckten oder digitalen Medien bedarf der Zustimmung der Bezirksregierung Düsseldorf.